Lecture Introduction과 Proof에 대해서

이 강의는 

1. 이산수학(Discrete Mathematics)의 기본적인 개념에 대한 강의이다.

2. 이산수학 구조, Discrete Mathematical Structure (numbers, graphs, trees, counting..)에 대한 것이다.

3. Discrete Probability Theory를 다룬다.

 

discrete의 의미는 무엇인가?

이산수학에서 '이산'이란 '이산가족'과 같이 따로 떨어져 있다는 의미로, '연속'의 반대의 개념이라고 보면 된다.

컴퓨터는 기본적으로 0과 1로 이루어진 데이터이기 때문에 '이산' 수학과 많은 연관이 있다.

 

Proof(증명)

가장 중요한 스킬은, 완전히 옳지 않을 매우 그럴듯한 주장을 완전히 옳은 proof와 구별할줄 아는 능력이다.

이것을 아는것이 수학의 기초이다.

 

피타고라스의 정리

Pythagorean theorem

변 a,b와 hypotenuse(빗변) c가 있을때 위 공식이 성립한다.

여러 증명이 있지만 다음과 같이 증명할 수 있다

 

같은 삼각형 4개와 임의 사각형을 c x c 사각형으로 배치시키고, a x a 사각형, b x b 사각형으로 다시 배치시킨다.

그럼 c x c 면적이 a x a 면적과 b x b 면적 합과 같아야 한다.

그러면 임의의 사각형이 b-a가 한변인 정사각형이 되고, 

위와 같이 배치시켜보면, a x a와 b x b가 c x c의 면적과 동일하므로 피타고라스의 정리를 증명할 수 있다.

 

하지만 이렇게 그림으로 증명하는것은 이 경우에는 맞지만, 일반적으로 그림으로 증명하는데에는 문제가 있을 수 있다. 

숨겨진 assumption이 있을수 있기 때문이다. 예를 들어서, 

위와 같이 11 x 10사각형이 있을때, 위 1 x 1의 이등변 삼각형을 잘르고 밀면, 10 x 11 사각형이 유지가 되면서 1 x 1의 사각형이 생겨난다. 금에 이를 적용시킴으로서 부자가 될수 있다.

이 증명이 틀린 이유는 두 이등변 삼각형은 45도가 아닌 대각선에 놓여져 있기 때문에, 정확히 맞는 삼각형이 아니기 때문이다. 이 사실을 실제로 감지를 못할수도 있기때문에 그림으로 증명하는 것은 위험하다.

 

또다른 가짜 증명은, 모든 다항식(Polynomial) ax^2 + bx + c에서 항상 2개의 근을 갖는다.

근의 공식에 따라서, 근은 r1, r2 두개를 갖지만

0x^2 + 0x + 1은 0개의 근을 가지고, 0x^2 + 1x + 1은 오직 하나의 근을 가진다.

여기서 bug는 a는 0으로 나눌 수 없기 때문에 a가 0이 되면 안된다 수정해야 한다.

또한 1x^2 + 0x + 0은 두개의 근이 아닌 하나의 근을 가진다. 

bug는 두 근이 같을때 하나의 근을 같는다. 따라서 D= b^2 -4ac 가 0이 아니여야만 한다로 수정해야한다.

하지만 D<0이면 어떠한가? x^2 +1은 i, -i의 근을 갖는다. 여기서 어떤게 r1이고 어떤게 r2인지 애매해진다.

근의 공식에 따르면  +v-1 -v-1인데, -1의 제곱근은 무엇인가? i와 -i의 차이점이 없다. 똑같이 작용하기 때문이다.

공식에는 문제가 없지만 이 애매모호함은 문제가 될 수 있다.

.

애매모호함이 있을때에는, 1과 -1이 같다는 것을 다음과 같이 증명할 수 있다.

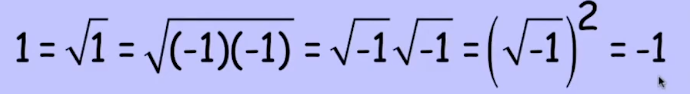
완전히 터무니 없다.

따라서 공식을 사용할 때에는 공식이 적절하게 사용되었는지 확인해야하고

생각없이 계산하는 것은 위험한 것이다. 이해를 해야한다. 위에서는 3번째에서 4번째로 넘어가는 것이 잘못되었다.

이렇게 1 = -1이 맞다고 잘못 증명해버리면, 양변에 같은것을 더하거나 곱하거나 양변이 같음으로, 양변을 1/2로 나눈다음에 3/2를 더하면 2와 1이 같다는 증명이 나온다.

 

 

 

reference : 

https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-042j-mathematics-for-computer-science-spring-2015/resource-index/

https://m.blog.naver.com/PostView.naver?blogId=junhyuk7272&logNo=221788873360&navType=by